L’énigme de Fermat passée au crible (1/4) : Fermat sur le Divan
Publié par Claude Mariotti, le 1 mai 2021 3.9k
"Le Voyageur contemplant une mer de nuages". Caspar David Friedrich
Sage parmi les fous,
dans la cité la rumeur,
et le ciel d'azur.
Pierre de Fermat vu par l'auteur.
NB : cette étude est beaucoup plus à jour ici, sur Wikiversité.
(1/4) : Fermat sur le Divan
(2/4) : Premier maillon, le coup de bluff
Fermat sur le Divan
« Cet homme remarquable, le premier d’entre nous, m’envoya deux propositions très subtiles, sans les accompagner de leurs démonstrations. Et alors que je lui demandais les démonstrations de ces propositions ardues, il me répondit, par lettre, en ces termes : « J'ai dû travailler pour les découvrir. Travaillez vous aussi ; vous prendrez ainsi conscience que c’est dans ce travail que consiste la majeure partie du plaisir. » Roberval à Torricelli, évoquant Fermat.
« La conviction profonde et partagée que Fermat n’a pas possédé une démonstration de son théorème vient de la longue histoire des tentatives faites pour l’établir. […] Les suiveurs des suiveurs, dans toutes les situations de ce genre, ne savent plus rien de ce qui a motivé les fondateurs […]. Ils pensent savoir tout ce qu’il y a à savoir, dès les commencements. » Jacques Roubaud, “Mathématique :” (1997).
« Quoi qu’il en soit, cette approche [d'Andrew Wiles], où le théorème de Fermat n’est qu’un corollaire très alléchant mais mineur, repose sur des techniques de représentations galoisiennes récentes. Reste possible qu’une démonstration élémentaire directe puisse être trouvée. » Catherine Goldstein, Un théorème de Fermat et ses lecteurs, p 120 (1995).
« Cette preuve de Fermat n’étant plus nécessaire aujourd’hui, était-elle suffisante en son temps ? » Roland Franquart (2009).
Cette étude est basée bien plus sur la pure réflexion, la logique, que sur l'arithmétique. N'y figure qu'un seul calcul, une courte multiplication. Si vous aimez les grandes et belles énigmes, et qu'en mathématiques vous avez un niveau, disons de quatrième, il suffit amplement. Avec Monsieur Roland Franquart qui en 2009 résolut cette énigme (elle datait de 1670), nous en avons fait l'étude complète. L'énigme n'avait jamais pu être déchiffrée avant que R. F. ne la découvre et s'y intéresse, c'est – aussi – ce qui en fait tout son sel. Quel mathématicien professionnel en effet aurait pu imaginer que Fermat ait pu crypter sa fameuse observation en 3 lignes 1/2 d'écriture latine ?! Qui d'autre qu'un latiniste grand amateur de math (R. F.), ancien militaire, technicien novateur travaillant dans les... radars ( !), aurait pu la mettre en lumière ? Le plus grand attrait de cette énigme est pour moi le magistral exploit de cryptage réalisé par Fermat. Cette étude je l'ai été écrite pour vous, et pour mon plaisir bien sûr. Elle a été initiée sur Wikiversité en 2019, les premiers jalons en ont été posés dès 2006. Après m’avoir procuré tant d’heureuses surprises, tant de joies, elle est maintenant terminée – presque en tout cas, car avec Fermat on en découvre toujours. Mon avis est que jamais un mathématicien n'est allé aussi loin dans la compréhension profonde, intime, des nombres. Je ne serais pas étonné que Catherine Goldstein, avec qui j'ai travaillé sur Wikipédia, soit aussi de cet avis. Il me faut attester ici, dans un devoir éthique fondamental, que je voue une reconnaissance éternelle à Pierre Fermat. Un grand merci à tous mes lecteurs, vos fréquentes visites m'ont encouragé et stimulé, sans vous cette étude n'aurait pu être aussi complète, aussi aboutie. Claude Mariotti, 25 août 2021
***
Avant la création de l'Académie des sciences par Colbert en 1666, alors qu'il n'existait pas d'institution mathématique, la coutume chez les mathématiciens était de se lancer des défis. Comme nous le verrons plus loin Fermat avait aussi testé 6 de ses principaux correspondants à propos de sa fameuse conjecture sur ce qu'on appellera plus tard les “nombres de Fermat”, pour laquelle il avait inventé la méthode lui permettant en quelques minutes de démontrer qu'elle était fausse. Le facétieux génie leur annonçait avec aplomb être (quasiment) assuré de sa véracité, mais il leur demandait... de lui fournir une preuve de cette validité. Pendant 19 ans, de 1640 à 1659, un par un, il les a ainsi testés. Aucun d'entre eux n'ayant pu ni prouver, ni invalider la conjecture, il a pu constater les limites de leurs compétences en la “science des nombres” (théorie des nombres). Ce fut d'ailleurs aussi le cas pour la plupart de ses autres défis, que personne ne voulut (ne put) relever. On a même prétendu que tous ces problèmes qu'il proposait, n’avaient absolument aucun intérêt. Malgré la facilité (pour Fermat en tout cas) à prouver la fausseté de la conjecture, il faudra attendre quasiment un siècle pour qu'enfin en 1732 le jeune Euler y parvienne. Finalement, plus aucun mathématicien contemporain de Fermat ne voulut le suivre — alors que ç’aurait grandement contribué à faire avancer la science. Il en fut contristé, amer et particulièrement fâché. Sa riposte, toute en pédagogie, fut à la hauteur de sa réputation, il lança un défi au monde. Selon nous, sa preuve étant si admirablement cachée grâce à la langue latine, il devait être assez assuré qu'on mettrait (très ?) longtemps avant de s'apercevoir qu'il l'avait « réellement dévoilée » (sane detexi). Et les mathématiciens, qui pensait-il, l'avaient bien mérité, auraient de quoi piétiner, s'arracher les cheveux et s'énerver pendant longtemps !
Dernier théorème de Fermat :
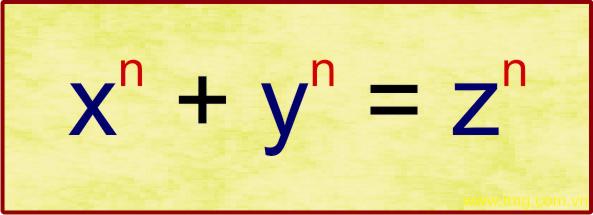
est impossible dès que n est un entier supérieur à 2.
Ce qui rend ce problème fascinant est la simplicité de son énoncé, alors qu'il est extrêmement difficile à résoudre. Pendant plus de trois siècles les plus grands mathématiciens ont tenté en vain de prouver la véracité de ce théorème, dont Pierre (de) Fermat dit, en 1670, avoir « réellement tissé, entièrement, l'explication tout à fait étonnante » (c'est la traduction après décryptage de sa deuxième ‘’OBSERVATIO‘’). Si cet Himalaya des mathématiques a pu être gravi après 324 ans d'efforts et d'espoirs déçus par Andrew Wiles en 1994, c'est uniquement par des moyens modernes et une voie très indirecte, au moyen d'une démonstration d'une complexité énorme, longue d'un millier de pages dans sa première mouture. Le 24 juin 1993, au lendemain de la conférence où Andrew Wiles écrit au tableau noir qu’il pense avoir prouvé la véracité du ‘’Dernier théorème de Fermat’’, le journal Le Monde annonce en première page : « Le théorème de Fermat enfin résolu ».The New York Times titre : « At Last, Shout of 'Eureka' In Age-Old Math Mystery » [1]. Mais le plus dur restait à venir pour Wiles, sa démonstration recelait une grosse faille.
La preuve de Fermat, beaucoup plus courte bien que très difficile à assimiler, n’a toujours pas été comprise par les Modernes. Voici une photo agrandie de l’«Observatio» de Fermat, observation qu'il écrivit on ne sait où au juste (il est douteux que ce soit dans une marge, comme nous le verrons plus loin) à propos de la conjecture qu'il affirme avoir prouvée (en 1636 lit-on généralement mais ce pourrait être un peu plus tardif). Cette photo se réfère à l'Arithmetica de la Bibliothèque de Lyon et elle attira l'attention de Monsieur Roland Franquart en 2009.

Avez-vous remarqué que le point (•) qui suit le mot “detexi” est plus gros que le point final, tout à la fin du texte ? Et diriez-vous que sur ce mot “de t exi” le «caractère» “t” est très exagérément surchargé, et fait davantage penser, si on l'isole du texte, à une tache, mais une tache qui aurait pu être finement exécutée de façon à être facilement assimilée, dans son contexte, à un “t” ? Ou au contraire diriez-vous que cette grosse surcharge sur un texte primordial de Fermat aurait été réalisée par un typographe je-m'en-foutiste, à la suite d'un défaut d'encre ? Deux originalités en tout cas, sur l'observation mathématique la plus importante de Fermat – et des mathématiques en général –, une OBSERVATIO insolite donc, à laquelle son fils, parfaitement conscient qu'elle deviendra célèbre sitôt diffusée, ne peut être étranger. Nous vous ferons découvrir tout au long de cette étude bien d'autres curiosités, en rapport soit avec cette observation, soit avec le grand théorème en lui-même, soit avec ce qu'on a coutume d'appeler les “nombres de Fermat”. Une autre curiosité qui m'avait rendu très perplexe pendant plusieurs mois après que je l'eus découverte est encore plus bizarre, et elle concerne cette même observation, ce même mot, imprimé dans des éditions différentes de celle-ci, comme par exemple celle que l'on trouve à l'Université de Rome[2]. Cette fois ce ne sera plus la lettre “t” qui aura été manipulée dans le mot, mais la lettre “i” , remplacée par le graphème ṡ :

Nous étudierons en détail ces deux premières anomalies de la note mathématique la plus célèbre de tous les temps, et dévoilerons 24 autres indices dont certains admirables d'ingéniosité
Les savants se sont toujours fiés à des traductions approximatives de cette note, qui toutes ont mal interprété, et dans toutes les langues, le mot “detexi”. C'est ainsi qu'en français on a traduit soit par “'j'ai trouvé”, soit par “j'ai découvert”. À l'heure où nous écrivons ces lignes (2 septembre 2021), on ne peut trouver nulle part une traduction fiable. Commençons donc par la traduire correctement en corrigeant cette première erreur :
- “J'ai trouvé”, ou “j'ai découvert”, ne se traduit pas par “detexi”, mais par “inveni”.
― Sur Dictionnaire Gaffiot, “invenio” (inveni, inventum, invenire) : trouver. Y voir aussi “inventio”': action de trouver, de découvrir, découverte.
― Sur Dictionnaire Olivetti, “trouver” : invenio (invenis, inveni, invenire, inventum).
- detexi :
― Sur Dictionnaire Olivetti : detego (detegis, detexi, detegere, detectum) : découvrir dans le sens de dévoiler.
― Sur Dicolatin : detego (detegis, detegere, detexi, detectum) : ôter ce qui couvre (mettre à découvert).
― Sur Dictionnaire Gaffiot : du verbe detego : découvrir, mais seulement dans le sens de mettre à découvert, mettre à nu, dévoiler.
En outre,
- sane : assurément, réellement, vraiment, entièrement, complètement (tout à fait).
- demonstratio sur Dictionnaire Gaffiot : action de montrer, démonstration, description.
Ci-dessous donc, la traduction correcte de l'«Observatio», qui reprend exactement le propos de Fermat. Nous verrons dans la section demonstrationem mirabilem sane detexi qu'une traduction encore plus affinée est possible et très utile. Le malicieux Pierre de Fermat, certain que son observation, qui rendait compte de sa plus importante découverte, serait mal traduite – même s'il ne pouvait imaginer tout ce qu'elle impliquerait pour les mathématiques des XXe siècle et suivants – a dû particulièrement s'amuser, tout comme son fils Samuel, en posant ce défi à des mathématiciens qui souvent, méprisant ses travaux, avaient fait de lui un vantard.
Pour l'instant cette première traduction qui conviendrait parfaitement à un bon latiniste nous suffit amplement :
« Mais que ce soit un cube en deux cubes ou bien un carré de carré en deux carrés de carré et en général jusqu'à l’infini, aucune puissance supérieure au carré ne peut être partagée en deux puissances du même nom, ce dont j’ai assurément dévoilé l'explication étonnante [ou admirable]. La marge trop étroite ne la contiendrait pas. »
Voici maintenant la traduction officielle d'Émile Brassinne (en bas de page), qu'on trouve dans son ouvrage Précis des œuvres mathématiques de P. Fermat et de l’Arithmétique de Diophante (Toulouse, 1853)]. Elle fut reprise en 2015 par Serge Coquerand dans son ouvrage À la (re)découverte des dix livres de l'arithmétique de Diophante, ainsi que par Bertrand Hauchecorne, qui l’exprime dans l'émission de France Culture Pierre de Fermat l’énigmatique (à 19’ 25’’), en 2015 également :
« Décomposer un cube en deux autres cubes, une quatrième puissance, et généralement une puissance quelconque en deux puissances de même nom au-dessus de la seconde puissance, est une chose impossible, et j’en ai assurément trouvé l’admirable démonstration. La marge trop exiguë ne la contiendrait pas. » L'ordre des mots est rigoureusement exact (adverbe devant participe passé). La seule (grosse) erreur concerne le mot detexi, traduit malencontreusement par “j'ai trouvé”, elle éloigne ainsi le lecteur d’une étude approfondie de l'observation. Extrêmement rares sont les commentateurs qui ont repris cette traduction officielle. On trouve au contraire des dizaines de fausses traductions dont la ligne générale est celle-ci :
« Il est impossible de diviser un cube en deux cubes, ou un bicarré en deux bicarrés, et en général une puissance quelconque supérieure au carré en deux puissances de même degré, j'en ai découvert une démonstration véritablement merveilleuse que cette marge est trop étroite pour contenir. »
Brassinne traduit parfaitement quand il écrit :
« et j'en ai assurément trouvé l'admirable démonstration. » Pourquoi, ensuite, les mathématiciens ont-ils “traduit” à leur manière en écrivant :
« et j'en ai trouvé la démonstration vraiment admirable (ou merveilleuse) » ? Échouant à retrouver la preuve qu'affirmait détenir Fermat, ils l'ont rendue encore plus extraordinaire qu'elle ne l'était. Les mathématiciens de l'époque de Fermat et ceux qui suivirent furent de plus en plus nombreux, à mesure qu'on échouait à retrouver sa preuve, à se désoler qu'il ne leur ait pas livré toutes ses démonstrations. De plus en plus la rumeur a couru qu'il ne vérifiait pas toujours ses conjectures. Diffuser cette mauvaise traduction, « démonstration vraiment merveilleuse », fut-ce une initiative intéressée ? En tout cas on penserait désormais que Fermat était encore plus fanfaron qu'on ne le pensait, et échouer à trouver une preuve n'avait finalement plus trop d'importance. L'histoire des mathématiques, et des sciences en général, est jalonnée de ces jalousies et mesquineries. Une autre fausse traduction a été rapportée par Jean Itard (1902-1979), qui fut professeur de mathématiques et l'historien. Il eut surtout une remarque particulièrement désagréable à l'encontre de Pierre de Fermat en écrivant en guise de conclusion à un court article en 1950 :
« Jamais Fermat n’a été en possession d’une preuve de son Grand Théorème pour un exposant supérieur ou égal à cinq. » C'est le commentaire le plus désobligeant qu'on puisse trouver sur Fermat. Le début de la phrase est péremptoire et violent : “Jamais Fermat”. Il poursuit en mettant deux Capitales d'imprimerie à ‘’Dernier Théorème‘’, manière radicale de démolir un théorème... capital. Jean Itard ne connaissant pas le latin, il s'était fié à une de ces nombreuses mauvaises traductions.
La propagation de ces fausses traductions eut deux effets :
– Tourmenter les savants pendant 324 ans (1994 – 1670 = 324) et non 358 ans (souvent arrondi en 350) comme on le lit souvent.
– Permettre que le plus grand défi de Pierre de Fermat – retrouver et comprendre entièrement l’admirable démonstration qu'il a réellement dévoilée en sondant « les mystères de la science des nombres » – n'ait toujours pas été complètement relevé en 351 ans (2021 – 1670 = 351).
Au lecteur
Dès que j'eus pris connaissance de la formidable énigme chargée d'histoire de Pierre de Fermat, je perçus que ce génie polymathe très inventif était suprêmement ingénieux, sûr de son fait et cerise sur le gâteau, très espiègle. J'avais un avantage non négligeable pour étudier le mystère qu'il nous proposait, ayant pour “allié” dans cette affaire Blaise Pascal (excusez du peu), qui encensait littéralement Fermat. Je souris intérieurement, et malicieusement, en pensant que toi amie lectrice, que toi ami lecteur, tu découvres en même temps que moi des choses passionnantes sur un immense génie du dix-septième siècle, des choses que la plupart des savants n'auront jamais sous les yeux. J'ai pourtant tenu à partager cette passion pour Fermat avec quelques rares scientifiques – mathématiciens, physiciens – que je savais réceptifs et leur ai mentionné cette étude, tous ont botté en touche d'une façon ou d'une autre. Si tu apprécies cette étude, alors peut-être souriras-tu en voyant qu'il n’est pas besoin d’être un éminent savant pour découvrir des choses admirables qui lui sont passées complètement inaperçues. En outre, je te prie de m'excuser de la longueur de cette étude, qui peut parfois être fastidieuse ; de m'excuser aussi de nombreux «quasi-doublons ». Grâce à de fréquentes relectures j'ai pu supprimer les nombreux «vrais doublons» autrefois présents, mais je confesse que cette recherche fut tellement passionnante qu'emporté par mon élan et ne voulant absolument rien omettre, il m'était difficile de faire plus court. Merci d'avance pour ta patience et pour ta compréhension. Et bonne lecture !
P-S : Si vous enseignez les mathématiques, ou même si vous êtes un simple passionné, il se peut qu'après avoir lu cet article vous ayez la tentation de le signaler à un mathématicien professionnel. Dans le meilleur des cas vous ne recevrez aucune réponse. Mais si vous rencontriez l'un d'entre eux et que vous avez apprécié cette étude, je vous suggère de réfléchir avant de l'évoquer devant lui, vous seriez immanquablement remis à votre place de “non-sachant” par une chicanerie ou par une autre : votre vis-à-vis aura tout d'un coup oublié ce qu'est la méthode scientifique, qui repose avant tout sur la rigueur. Mais vous pouvez toujours courir le risque...
Fermat en effet utilise dans son début d'explication le “Triangle de Pascal” et s'est vu obligé, à l'aide de très subtils codages, d'être encore plus elliptique qu'à son habitude...en 3 lignes 1/2 de latin ! Aucun savant à ma connaissance n'a réussi à “combler les trous” dans son explication, je me demande même s'il y a eu la moindre tentative sérieuse – approfondie – en ce sens.
Avant-propos
L’objectif de cette étude sera de faire état de tous les arguments trouvés en faveur de l’existence d’une preuve du grand théorème par Fermat lui-même.
Bien qu’ayant nourri depuis longtemps un goût prononcé pour la mathématique et la physique (ah ! la découverte, dans ma jeunesse, des intégrales, de la dynamique des corps, des si belles, si simples, si logiques formules), je ne suis pas mathématicien, seulement un anonyme un peu polymathe, un peu philosophe et surtout un insatiable curieux.
De nombreux mathématiciens, professionnels et amateurs, se sont passionnés pour cette énigme, imaginant une démonstration “élémentaire” (courte) à leur portée. Las, cette simplicité apparente pose un voile sur des difficultés insoupçonnées. Pendant longtemps les savants ont été envahis de courriers accompagnés d'une démonstration, bien sûr toujours fausse (on trouve encore à peu près chaque semaine une nouvelle pseudo-démonstration sur internet). En 1908, Paul Wolfskehl avait créé un prix de 100 000 marks pour récompenser le premier qui trouverait une preuve au théorème. Des démonstrations plus ou moins farfelues commencèrent à s’accumuler sur le bureau du professeur Edmund Landau, chef du Département des mathématiques à l’université de Göttingen, qui avait été chargé d’examiner toutes ces propositions de preuve. Leur nombre augmenta tellement que son travail personnel en pâtit. Il fit alors imprimer en grande quantité des modèles de réponse prêts à l’emploi :
Cher…
Je vous remercie pour votre manuscrit sur la démonstration du Dernier théorème de Fermat. La première erreur se trouve : page… , ligne… Cela infirme la démonstration.
Professeur E.M. Landau
Puis il pria ses élèves de remplir les blancs.
Martin Gardner évoque un ami mathématicien qui répondait à chaque expéditeur :
« N'étant pas moi-même compétent pour analyser votre démonstration, je vous encourage à l'envoyer à Monsieur..., expert en la matière et qui pourra vous aider. Voici son adresse : ... ».
L'expert en question n'était autre que le dernier expéditeur d'une démonstration.
Dans les années 1970 l'effet de découragement de ces 350 années d'échecs relatifs était tel qu'il était de bon ton de dire que l'assertion de Fermat n’était pas suffisamment générale pour être considérée comme significative ou qu’elle était soit indémontrable soit fausse. Mais en l'espace d'une trentaine d'années la communauté mathématique a radicalement changé sa perception de la question en passant d'un désintérêt plus ou moins courtois à l'enthousiasme le plus vif ! On s'est soudainement mis à croire à la véracité de l'assertion de Fermat vers 1985 et cette disposition d'esprit a été un puissant stimulant pour l'édification des difficiles théories qui ont conduit à sa démonstration. Yves Hellegouarch.
Déjà avant 1994 il semble que l’inconscient collectif et l’effet de groupe à l’œuvre dans les hautes sphères de la discipline aient décidé qu’il faille arrêter là les dégâts et disqualifier encore plus, et par tous les moyens possibles Fermat et son théorème. Rendons ici hommage aux nombreux savants qui ont fait preuve de sagesse et de retenue. La découverte d'une démonstration par Wiles en 1994 suscita l'enthousiasme dans le monde entier, un enthousiasme parfois mâtiné d'un peu de tristesse : pour prouver un énoncé très élémentaire il avait fallu écrire tout un traité de mathématiques, d’une difficulté inouïe. Jamais un mathématicien bien comme il faut n’aurait imaginé que Fermat (dont l'espiègle pédagogie était pourtant bien connue) ait inséré dans sa deuxième observation (outrageante ?) écrite en latin, tout ce qui était nécessaire pour la décrypter.
Nos mathématiciens ne savent plus raisonner sainement sur les concepts primordiaux, n’y ayant jamais été contraints puisque leurs prédécesseurs, de plus en plus ont brûlé les étapes. Ils sont en conformité avec l’époque, une ère matérialiste. L’esprit est de plus en plus encombré de pensées compliquées, tout comme l’est leur manière de chercher. Pour raisonner ils recourent à de plus en plus de symboles mathématiques, de formules de plus en plus complexes, leur pensée s’appuie sur cette complexité au lieu que d’être une pensée pure. L'abstraction dans le simple est devenue inaccessible, le pur spirituel, sa beauté, sont définitivement perdus.
Citons Alexandre Grothendieck (RÉCOLTES ET SEMAILLES – Réflexions et témoignage sur un passé de mathématicien) :
« Nos esprits sont saturés d’un « savoir » hétéroclite, enchevêtrement de peurs et de paresses, de fringales et d’interdits ; d’informations à tout venant et d’explications pousse-bouton – espace clos où viennent s’entasser informations, fringales et peurs sans que jamais ne s’y engouffre le vent du large. Exception faite d’un savoir-faire de routine, il semblerait que le rôle principal de ce « savoir » est d’évacuer une perception vivante, une prise de connaissance des choses de ce monde. Son effet est surtout celui d’une inertie immense, d’un poids souvent écrasant. Le petit enfant découvre le monde comme il respire – le flux et le reflux de sa respiration lui font accueillir le monde en son être délicat, et le font se projeter dans le monde qui l’accueille. L’adulte aussi découvre, en ces rares instants où il a oublié ses peurs et son savoir, quand il regarde les choses ou lui-même avec des yeux grands ouverts, avides de connaître, des yeux neufs – des yeux d’enfant.
Il arrive que l’un ou l’autre de nous découvre telle chose, ou telle autre. Parfois il redécouvre alors dans sa propre vie, avec émerveillement, ce que c’est que découvrir. Chacun a en lui tout ce qu’il faut pour découvrir tout ce qui l’attire dans ce vaste monde, y compris cette capacité merveilleuse qui est en lui – la chose la plus simple, la plus évidente du monde ! (Une chose pourtant que beaucoup ont oubliée, comme nous avons oublié de chanter, ou de respirer comme un enfant respire…). Chacun peut redécouvrir ce que c’est que découverte et création, et personne ne peut l’inventer. Ils ont été là avant nous, et sont ce qu’ils sont. »
Les mathématiques, surtout celles de Fermat, sont aussi une philosophie. Cette recherche fait appel à de nombreuses disciplines, mathématiques, histoire des math, philosophie (dont la logique philosophique), psychologie, sociologie, linguistique, pédagogie, didactique. La question considérée aide d'ailleurs à comprendre notre époque. Appréhender la psychologie d'un tel personnage pour tenter de découvrir tout ce qu'il a voulu signifier par ses astuces littéraires fut un long travail. Ce n'est qu'au fil des découvertes (on va de surprise en surprise) et au prix de longues méditations (entrecoupées de temps “morts”, que nous pûmes progresser. ce fut difficile au début car l'imaginaire collectif est là, qui sans cesse rappelle le jugement définitif qu'ont porté quelques grands savants à l'encontre de Pierre de Fermat et de son théorème. Cette recherche fut effectuée principalement sur une période de 18 mois, de janvier 2019 à mai 2020.
L’histoire du ‘’Dernier‘’ théorème commence aux alentours de l’année 1638. Fermat est alors âgé d’une trentaine d’années. On peut mieux comprendre son inextinguible soif de connaissances en considérant qu'il vit à une époque où, sans rien renier des connaissances des Anciens, au contraire en les admirant, on s'attache à leur étude pour mieux aller de l'avant. Tout est digne d'intérêt on est polymathe. Fermat est de ces hommes, humaniste, lettré, mathématicien (dès qu'il a du temps libre), philologue, il connaît le latin, le grec et l'italien, fait des vers français, latins, espagnols. Natif de Beaumont-de-Lomagne dans le Tarn-et-Garonne, il s'installe d'abord à Bordeaux, puis à Toulouse, faisant carrière dans la magistrature où il s'acquitte de sa tâche d'une manière exemplaire. Lorsqu'il découvre l'arithmétique des Anciens, il y voit une telle intelligence, une telle stimulation pour l'esprit, que se contenter d'une activité rémunérée ayant surtout l'avantage d'assurer sa subsistance n'est même pas une question à se poser. Il voit dans l'étude des nombres la voie royale pour contempler les mystères de la Nature. Son enthousiasme débordant a trouvé là le moyen de s'exprimer et sa voie est toute tracée. Grâce à lui la connaissance pourra s'accroître et se propager. La science des nombres n'est pas sa seule passion, le latin, langue des savants et des lettrés, n'a aucun secret pour lui. « Il fut façonné par la rigueur et l’intelligence latines : c’est sur ce terreau que put s’épanouir son prodigieux génie des mathématiques. » Il est très croyant, comme en témoigne son poème latin ‘’Soumets-toi à Dieu ou l'agonie du Christ‘’ dédié à Jean-Louis GUEZ de BALZAC. Au début du poème, la raison est engagée à renoncer aux vaines divinités des fables et à se soumettre à Dieu. Fermat est un juriste discret, et bien qu'il fût un génie, « le plus grand homme du monde » selon Blaise Pascal, on sait peu de choses de sa vie. Et on ne connaît que quelques très rares démonstrations qu'il voulut bien livrer, une des plus remarquables étant celle où il démontre que le nombre 26 est le seul de tous les nombres à être compris entre un carré et un cube : 25 (5x5), et 27 (3x3x3).
Un jour, alors qu'il est en contemplation devant la beauté du théorème de Pythagore (a²=b²+c²), il s'interroge. Pourrait-on ajouter encore quelque chose au sujet, quelque chose auquel personne n'aurait jamais pensé ? Dans la formule de Pythagore, l'exposant est le nombre 2, le seul nombre qui élevé au carré soit égal à son double (2² = 2+2). Fermat a pu penser que cette propriété lui conférait des propriétés très particulières, et il a l'idée qui allait bouleverser les mathématiques pour les siècles à venir. L'impensable se produit, il remplace l'exposant 2 par un 3. Est-ce que l'égalité pourrait encore exister pour certains cas en choisissant avec soin les valeurs de a, b et c ? On perçoit déjà l'étendue de ses ambitions. A priori il ne semblait pas que ce fût possible, on pouvait toujours s’en approcher de très près, parfois même à une unité, mais trouver une solution semblait impossible. Le nombre 2, monstre mathématique, semble le suggérer : à l'Unité, on a ajouté l'unité pour en faire une double unité, une manipulation philosophiquement blasphématoire – ou merveilleusement créatrice. Non seulement 2 est le premier des nombres premiers, mais il est aussi le seul nombre premier à être pair. Pour Fermat, tenter de prouver l'impossibilité de son égalité serait un défi formidable, et c'est tout ce qu'il lui faut. Il se rend compte assez vite qu’il serait plus facile de tester d'abord sa méthode avec un 4 en exposant, le carré de 2, ce nombre qui semble narguer tous ses suivants. Il utilise une méthode qu'il nomme ‘’descente infinie’’, ou descente indéfinie, un raisonnement par récurrence et un autre par l'absurde, le tout extrêmement efficace. Sa méthode fonctionne parfaitement avec l'exposant 4, plus difficilement avec 3. En septembre 1636 il commence à exciter la curiosité de ses correspondants, dans une lettre à Mersenne pour Sainte-Croix où il propose ce défi : « Trouver deux puissances quatrièmes dont la somme est une puissance quatrième et deux cubes dont la somme est un cube ».
À partir de l'exposant 5 et jusqu’à l’infini, il comprend vite que la méthode n'est plus adaptée. Il lui faut trouver une autre voie, qui très certainement n’aura aucun rapport avec la première. En 1670, cinq ans après sa mort, dans une courte “OBSERVATIO” provocatrice écrite en latin, tenue jalousement secrète de son vivant et que son fils Clément-Samuel fait connaître, il affirme avoir « assurément dévoilé une explication tout à fait étonnante que la marge trop étroite ne saurait contenir ». À cette observation Samuel en a ajouté 47 autres, le tout est inséré aux endroits adéquats dans le Livre VI de l’Arithmetica du mathématicien grec Diophante d'Alexandrie (publiée en 1621), et où Bachet de Méziriac avait ajouté une traduction du grec au latin. On dispose donc en 1670 d'une nouvelle Arithmetica, légèrement augmentée mais ô combien précieuse pour la suite. L'observation en question se rapporte à la question VII, c'est la deuxième des 48 et elle se distingue notablement des autres. Nous y reviendrons.
Chez les Anciens on n’était pas sollicité dès le plus jeune âge par toutes les vanités qui encombrent maintenant l’esprit de nos enfants. De grandes intelligences ont pu ainsi atteindre à un grand savoir en pénétrant l’essence des choses (Socrate, Euclide...). Bien plus tard et dans un même siècle, Pascal, Leibnitz et Fermat qui fut un fameux exemple en théorie des nombres, construisant de puissants raisonnements avec parfois le seul recours aux mots. Comme Pythagore et comme Euclide, comme Diophante aussi, autre immense génie, Fermat sait que quand l’homme a posé 1, puis 2, tout est déjà posé, l’unicité, la pluralité du monde. Quelque chose a dû spécialement lui plaire avec ce premier nombre pluriel pour rendre le théorème de Pythagore décidément inégalable par sa puissance, sa singularité, et pour imaginer une conjecture beaucoup plus plurielle. Il fallait mettre sur un des deux plateaux de la balance les plus importantes propriétés du premier nombre entier suivant l’unité, l'unité doublée donc. Puis trouver et placer sur l’autre plateau une nouvelle conjecture qui soit en rapport avec la première, mais appelant cette fois l’infinité des nombres entiers (remarquons que 1, le nombre unitaire, n’est pas directement présent dans la «comparaison», il est “à part”). Peser le pour et le contre semblait a priori un défi gigantesque. Très vite Fermat voit que les deux plateaux de la balance ne pourront jamais se trouver à la même hauteur, une mise en abyme est impossible. Il va s’attacher à le prouver.
La question du Dernier théorème est bien plus qu’une question arithmétique. Son histoire est un marqueur profond de l'historiographie des Mathématiques. En reprenant l'idée de Eric Temple Bell il y a de bonnes chances que la civilisation s'étengne avant que les mathématiciens modernes aient complètement assimilé l'explication de Fermat.
Genèse de l'étude
La première lecture (vers 1997) qui m'a fait m'intéresser à ce problème est celle du célèbre ouvrage de vulgarisation de Simon Singh, Le dernier théorème de Fermat, lecture qui m'avait été suggérée par une amie étudiante en mathématiques. J'ai tout de suite sentie que je tenais quelque chose de beau et d'important[3], même si je n'avais aucune idée de ce que je pourrais y apporter de nouveau. Baudelaire écrit dans un de ses petits poèmes en prose : « J’aime passionnément le mystère parce que j’ai toujours l’espoir de le débrouiller. » J'ai moi aussi cette passion poussée à un haut degré. Souvent on considère un mystère comme insoluble, par la raison même qui devrait le faire regarder comme "facile" à résoudre. Mais concernant cette énigme c'est peut-être seulement vers 2010 que je découvris le premier gros indice, une formulation un peu ambigüe de Fermat dans sa dernière lettre à Carcavi où il cite sa fameuse fausse conjecture. Je pressentis que j'allais avoir affaire à forte partie (eh oui, c'était Fermat). Il cachait certainement beaucoup de choses, mais puisqu'il avait déjà laissé de nombreux indices dans sa note (complexes, ceux-là, découverts par Roland Franquart en 2008/2009, que nous évoquerons plus loin), il était tout à fait possible qu'en étudiant sérieusement ses travaux, ses correspondances, et en cherchant aussi à comprendre au mieux sa personnalité, on trouve d'autres indices plus simples d'accès. Je compris que ce n’était pas des réponses qu’il fallait chercher, mais des questions, et de bonnes questions. Je trouvai d'abord celles-ci :
- Fermat était-il ingénieux au point d'avoir pu trouver, en faisant un pas de côté, une preuve «simple» (avec beaucoup de guillemets), très courte, très profonde et complexe, très éloignée aussi des méthodes du calcul traditionnel ?
- Surtout, pourquoi tout est-il si bizarre autour de ce théorème ? Avait-il une ou plusieurs raisons d'être souvent si mystérieux ? Par exemple :
- Pourquoi sa plus célèbre observation est-elle écrite sur le mode de la plaisanterie, encore davantage que dans d'autres ? Pourquoi aussi paraît-elle aussi insolente ?
- Pourquoi la fausse conjecture sur les nombres de la forme 22n + 1, la dernière fois qu'il la formule, l'écrit-il sous une forme ambigüe qui laisserait croire à ceux qui refuseraient de lui faire confiance, qu'il la croyait vraie, et que donc il ne serait pas fiable sur tout le reste ?
- Comment se fait-il aussi que son Arithmetica – socle de tout son travail (où, nous dit son fils, il avait écrit dans les marges ses 48 observations) et qui devient, surtout après la découverte de l'énoncé de son grand théorème, un document historique d'une valeur considérable, a disparu ? Pourquoi son fils Clément Samuel ne l'a-t-il pas conservée ? Avait-il une bonne raison pour cela ?
- Ne faudrait-il pas analyser en profondeur tout ce qui tourne autour du théorème et de sa fausse conjecture ?
- Fermat est-il un honnête homme ? Certainement, alors pourquoi ne pas commencer par lui faire confiance ?
- Pourquoi au contraire certains commentateurs ne lui ont-ils pas fait confiance et l'ont-ils autant déprécié ?
En faisant preuve du simple bon sens, dans une approche objective dénuée de tout préjugé, à mesure qu’on progresse dans la recherche nos découvertes nous apportent un lot de satisfactions inestimable, c'est un merveilleux cadeau qu'on se fait à soi-même. Qui a l'esprit de discernement sait faire preuve de confiance, d'humilité et d'audace, d'analyse rigoureuse, d'imagination créatrice, toutes aptitudes nécessaires pour résoudre les plus difficiles énigmes. Je crois que la résolution des grandes énigmes, soit que la notion d’infini représente une pièce essentielle du mystère, soit qu'elle en soit absente, est presque toujours possible – ou au moins largement abordable. Mais dans ce cas-ci j'avais beau chercher, presque toujours avec le même enthousiasme, je ne trouvais d'abord que quelques nouveaux indices de-ci de-là. Il est vrai qu'en les assemblant ils me confortaient dans mon intuition initiale, et même s'ils n'aboutissaient à rien de concret ils constituaient déjà, après à un survol objectif du contexte général plusieurs fois réitéré (où j'incluais les mots de Fermat mais aussi ceux de tous ses détracteurs), un bon début d'analyse. Il me fallut attendre une douzaine d'années avant de recevoir un message privé via Wikipédia d'un mathématicien amateur (Roland Franquart) qui allait complètement débloquer la situation. Nous nous sommes téléphoné et je crois que nous avons conversé plus d'une heure. Par la suite nous avons beaucoup échangé et travaillé sur un blog dédié où une doctorante était intervenue. Puis j'ai continué à tenter de rendre l'article de Wikipédia sur le théorème un peu plus fiable sans parvenir à grand-chose, une vive opposition m'en empêchant. Quand je retournai en 2013 sur l'encyclopédie après une longue absence je fus tout de suite encouragé par Catherine Goldstein, mais je quittai pourtant à nouveau Wikipédia pour me consacrer entièrement à mes recherches. Je ne me doutais pas alors qu'en étudiant cette énigme avec un esprit très libéré j'allais beaucoup progresser au fil de trouvailles de plus en plus étonnantes qu'après Roland Franquart j'allais faire à mon tour. Je dois à la justice de dire que sans ses découvertes je n'aurais rien trouvé de neuf, toute cette recherche n'aurait pu se faire. À tout seigneur, tout honneur !
Vers 2006, après avoir consulté la fiche Wikipédia concernant ce théorème j'avais remarqué qu'aucun des arguments avancés par les contempteurs de Fermat ne tenait la route. Nombreux sont les scientifiques contemporains, toutes disciplines confondues, qui raisonnent avec une forme de pensée magique et font preuve de condescendance, quand ce n'est pas un mépris affiché envers les Anciens. Cette condescendance fait partie des mœurs courantes des mathématiciens accomplis. Dieu sait si je suis averti pour dire combien il peut y avoir de personnes bardées de diplômes comme autant de certitudes, de ces personnes que la reconnaissance académique conforte dans leurs béates certitudes. La question évidente à se poser en voyant la façon étonnante dont avait été rédigé l'article de Wikipédia était « Pourquoi ? ». C'était la première pierre à soulever impérativement pour ne pas être contaminé par le pessimisme ambiant et partir du bon pied. Cette conformité jalouse et exacerbée avec la pensée commune étant évidente j'ai voulu d'abord répertorier les mauvais arguments et leurs conséquences néfastes, qu'au cours des siècles les contempteurs de Fermat avaient pu imaginer. Ensuite, puisqu'il avait lancé son défi, il me fallait tout faire, puisqu'ayant assez vite perçu ses manières j'admirais sa clairvoyance, pour relever son défi. Non pas le défi mathématique en lui-même puisque je ne suis aucunement mathématicien, mais le défi de percer tous les secrets que dans ses divers écrits relatifs au théorème et à la fameuse fausse conjecture il aurait pu dissimuler. La difficulté était qu'il n'en disait jamais plus que nécessaire, les meilleurs signaux qu'il envoyait étant les plus difficiles d'accès. Ainsi est née cette recherche, très laborieusement d'abord. Tenter de résoudre de la façon la plus exhaustive possible cette formidable énigme, qui exige une analyse poussée de la psychologie de Fermat et de ses nombreux écrits, qui demande une conscience aigüe de sa sagacité, a suscité chez moi enthousiasme et excitation. Si j'avais été mathématicien, jamais je n'aurais pensé à chercher avec autant de foi et de persévérance tous ces arguments – qui faisaient bien plus appel au simple bon sens qu'aux mathématiques – pour réhabiliter Fermat et son dernier défi, j'eus été empêché, par des préjugés et une manière conformiste de raisonner, de sortir des sentiers battus et rebattus pendant des siècles, qui avaient abouti à une incroyable imposture scientifique : « Fermat n'a pas pu trouver de preuve, puisqu'il ne connaissait pas nos outils modernes ».
Les techniques sophistiquées qu'utilise le mathématicien contemporain exigent un long apprentissage, beaucoup de travail, elles occupent tout son temps. Ses contraintes professionnelles ne lui permettent plus de se consacrer à une question qui lui semble de si peu d'intérêt. Pour détricoter une pareille énigme c'est le pédagogue singulier, le combattant isolé, qu'il nous fallut convoquer. Son arme de prédilection est le défi. Mais pour que les mathématiciens qui le suivront ne soient quand même pas trop furieux, il ne doit pas les défier trop ouvertement. Il trouve alors deux nouvelle armes, la facétie et la ruse, et il en use à profusion. Pour avoir une chance de relever le défi, il fallut aller directement à la source, trouver puis exploiter la traduction la plus exacte, la plus fidèle possible de l'OBSERVATIO. Ensuite et en espérant qu'il n'en était pas resté là, il fallut continuer de chercher avec une obstination sans faille toutes les autres pistes qu'il aurait pu laisser. Ce fut long, semé d'embûches, souvent grisant.
« L'historien ne doit rien refuser d'entendre. » (Cicéron)
Voici la traduction de l'épitaphe de Pierre de Fermat :
« À la pieuse mémoire de Pierre de Fermat, membre du parlement de Toulouse.
Très versé dans les belles lettres, dans la connaissance des langues, des mathématiques et de la philosophie, il se montra jusrisconsulte éminent et remplit sa charge avec tant de distinction qu’il semblait avoir concentré sur l’étude des lois toutes les forces de son esprit, bien qu’il les divisât entre les spéculations les plus ardues. Ennemi du vain étalage, il négligea de livrer ses travaux à l’impression ; plus grand encore par le dédain que par la production, il lut, sans orgueil, dans les livres d’autrui, la glorification de ses œuvres. Aujourd'hui parvenu, comme ses vertus nous donnent le droit de l'espérer, à contempler la vérité éternelle et à mesurer toutes choses, grandes et petites, à la clarté d'un rayon céleste, il semble, de son tombeau, adresser au passant ce précieux conseil de morale chrétienne : Vis scire quiddam quod juvet ? nesciri ama. (Traduction : « Veux-tu ne pas ignorer ce qui est utile ? Aime être ignoré. »).
OB . XII . IAN . MD.C.LXV . AET . AN . LVII. » (Traduction : Il mourut le 12 janvier 1665 à l'âge de 57 ans). Pierre Fermat est donc né en 1608, ce qu'avait déjà relevé Émile Brassinne dans son Précis des œuvres mathématiques de P. Fermat et de l’Arithmétique de Diophante (cette page 10, note de bas de page).
Sur l'année de naissance de Fermat
Nous avons vu que Fermat naît en 1608 (avec une petite marge d'incertitude, une naissance dans les 12 premiers jours de 1609 est aussi possible) et décède à l'âge de 57 ans. Une seconde traduction du texte latin, avec la formule utilisée aux temps anciens est correcte : « Il mourut 12 janvier 1665 dans la cinquante-septième année de son âge ». Jadis en effet si l'on pouvait par exemple dire : “Fermat est né à Beaumont”, en revanche la phrase “Il mourut à 57 ans” n'avait pas de sens. Le mot “âge”, en latin AETAS (temps de la vie, âge de la vie) devait prendre place, et on utilisait la formule ‘’dans la Nième année de son âge’’. De nos jours cette seconde traduction prête à confusion car on pourrait comprendre “Il mourut alors qu'il entamait (était entré dans) sa cinquante-septième année” (à 56 ans donc). Alors que c'est inexact, voyez par exemple cet extrait d'un ouvrage ancien : « L’infortunée princesse n’avait pas atteint la première année de son âge, et déjà elle pardonnait aux plus cruels ennemis de sa famille ». Quelques auteurs font la confusion et annoncent 1607 comme année de naissance. Cette erreur s'est répandue jusqu'à nos jours, le plus souvent sous la forme « né en 1607 ou 1608. »
On croirait presque que du lieu de félicité où il s’émerveille encore de tout ce qu’on dit, c’est Fermat lui-même qui se plaît à alimenter son épitaphe
« Veux-tu ne pas ignorer ce qui est utile ? Aime être ignoré. »
Les Anciens étaient parvenus à extraire d’une gangue arithmétique informe les grands concepts principaux sans disposer de tout le symbolisme algébrique aujourd'hui disponible. Pierre de Fermat, comme ses contemporains mais à un degré plus élevé, a maîtrisé l’art de contourner les difficultés auxquelles se heurteront ceux qui viendront après lui, au point de pouvoir se passer de nombreux outils mathématiques qui seront découverts bien plus tard. Nous trouvons maintenant évidents des concepts primordiaux que ces Anciens ont découverts. Jusqu’au siècle dernier, et même encore parfois de nos jours, ce caractère d’évidence a engendré chez quelques savants, quand ils ont eu à ferrailler avec Pierre de Fermat, leur Maître pourtant, une coupable négligence – une arrogance parfois.
Si aller à l'encontre de tous les jugements négatifs qui ont été portés à son encontre n'est pas aisé, deux choses aident à garder intacts l'enthousiasme et la confiance.
- On sait d'une part qu'il disposait de très peu de temps pour assouvir sa passion des nombres. Ce n'est qu'en gardant par devers lui la grande majorité de ses inventions au fur et à mesure qu'il les faisait, qu'il pouvait préserver sa tranquillité et exploiter tout son potentiel créatif. S'il avait commencé à rédiger des démonstrations complètes de ses inventions, la compréhension en ayant été ardue, des esprits tatillons lui auraient fait perdre son temps avec d'incessants chipotages. La formulation de ses défis, qui souvent ne comportaient que quelques lignes, ce qui pouvait paraître inconvenants de la part d'un notable, témoignait aussi de ce cruel manque de temps.
Alors qu'il a affirmé dans sa correspondance posséder la preuve du cas particulier n=4 de son grand théorème, il ne nous dit pas explicitement, dans l'Arithmetica, quelle est cette preuve. Il livre sa démonstration du “Théorème de Fermat sur les triangles rectangles” sans du tout préciser qu'elle a un rapport quelconque avec le cas n=4. Or de ce théorème on infère immédiatement la preuve de ce cas, c'est la seule démonstration qu’il révèle – dans ses 48 observations en tout cas. Pour quelle raison alors n'évoque-t-il pas ce cas n=4, si ce n’est pour indiquer qu'il a placé là une première balise et qu'il faudra nous attacher à en chercher d'autres, mieux cachées encore, dans tous ses écrits. Ainsi il ne faudra pas prendre à la légère : a) son défi plusieurs fois réitéré sur le cas particulier n=3, jusqu'à son affirmation, finalement, qu'il a fait la preuve de l'impossibilité de ce cas ; b) son affirmation d'avoir assurément dévoilé l'explication étonnante (ou admirable) de son théorème général. Qu'il se soit abstenu de mentionner le cas n=4 dans sa démonstration nous semble être le tout premier des arguments en faveur d’une maîtrise complète, par Fermat, de la situation : il sait de quoi il parle et nous le fait savoir. On est assuré par ailleurs qu'il possède effectivement la preuve du cas n=3, mais là encore, alors qu'il n'a cessé dans parler dans ses lettres, il passe complètement sous silence ce cas dans les 48 observations.
Sûrement avait-il aussi une revanche à prendre sur la communauté des mathématiciens (« Ah ! ils n'ont pas voulu me prendre au sérieux ? Eh bien ce n'est plus à ces esprits négligents que je penserai dorénavant. »). S'est-il dit aussi : « Nous allons bien nous amuser. » ? Sans doute. Certains de ses correspondants en effet à qui il avait soumis des problèmes qu'ils avaient été incapables de résoudre, avaient méprisé ses travaux, les jugeant totalement inutiles (ils se révélèrent pourtant d'une importance considérable). Il en fut certainement contrit au point de vouloir les punir de leur négligence. La nature de son caractère dut aussi y être pour quelque chose, on le savait très humble, mais il était parfaitement conscient de sa force, et la fausse humilité était étrangère à ce Gascon. Une démonstration complète d'un cas particulier (n=3) de son grand théorème ne sera trouvée que deux siècles plus tard par Gauss, un autre immense mathématicien. Gauss qui écrivait en 1801 à propos du petit théorème de Fermat : « Ce théorème remarquable, tant par son élégance que par sa grande utilité, s'appelle ordinairement théorème de Fermat, du nom de l'inventeur. » Cet intérêt de Gauss pour le travail de Fermat fut d'ailleurs en partie à l'origine de sa future carrière de mathématicien. Par ailleurs, en citant E.T. Bell, « Gauss discréditait les assertions sans fondement. » Un ami de Gauss lui avait demandé pourquoi il ne concourait pas pour le prix offert en 1816 par l’Académie française des sciences qui récompenserait le découvreur d'une preuve (ou d'une invalidation) du Dernier Théorème. « J’avoue, répondit-il, que le Théorème de Fermat est une proposition isolée qui a très peu d’intérêt pour moi, puisque je pourrais facilement trouver une multitude de propositions du même genre, que personne ne pourrait jamais ni valider ni invalider [...]. Bien qu’il ne l’ait jamais dit explicitement, Gauss semblait douter que Fermat avait prouvé son théorème. » Gauss n'a-t-il jamais essayé de prouver cette conjecture ? Ça peut sembler étonnant.
- D'autre part, beaucoup des écrits les plus importants de Fermat sont rédigés en latin, la langue de l'ellipse par excellence. Fermat étant expert en cette langue, il nous a fallu débusquer le plus possible de ses non-dits – écrits, mais subtilement cachés – auxquels l'obligeaient : a) le manque de temps ; b) le souci de discrétion dans une époque troublée (alors même qu'il est magistrat) ; c) le principe même du défi, qui s'accordait avec les deux points précédents ; enfin, d) son goût pour la pédagogie, qui s'accorde à son tour avec les points précédents. Quatre raisons donc d'en dire le moins possible...
Lorsqu'on étudie Fermat, il y a deux façons de procéder :
1) Avec un a priori favorable : lui faire confiance, toujours se souvenir que c’est un grand pédagogue, rechercher sans relâche des indices, et finalement tous les bons arguments (nous en avons dénombré plus de 26) an faveur de l'existence d'une preuve à son grand théorème. Notons que quasiment tous les auteurs ayant publié un livre consacré à ce théorème ont eu la sagesse de rester objectifs.
2) Avec un a priori très suspicieux : le sous-estimer, occulter son désir le plus cher de ne jamais nous mâcher le travail. On imagine alors n'importe quel "argument" pour le discréditer. Citons Alexandre GROTHENDIECK :
« L’aspect de cette dégradation auquel je pense surtout ici (qui en est juste un aspect parmi de nombreux autres) est le mépris tacite, quand ce n’est la dérision sans équivoque, à l’encontre de ce qui (en mathématique, en l’occurrence) ne s’apparente pas au pur travail du marteau sur l’enclume ou sur le burin – le mépris des processus créateurs les plus délicats (et souvent de moindre apparence) ; de tout ce qui est inspiration, rêve, vision (si puissantes et si fertiles soient-elles), et même (à la limite) de toute idée, si clairement conçue et formulée soit-elle : de tout ce qui n’est écrit et publié noir sur blanc, sous forme d’énoncés purs et durs, répertoriables et répertoriés, mûrs pour les ‘’banques de données’’ engouffrées dans les inépuisables mémoires de nos méga-ordinateurs. Il y a eu (pour reprendre une expression de C.L. Siegel) un extraordinaire ‘’aplatissement’’, un ‘’rétrécissement’’ de la pensée mathématique, dépouillée d’une dimension essentielle, de tout son ’’versant d’ombre’’, du versant ‘’féminin’’. Il est vrai que par une tradition ancestrale, ce versant-là du travail de découverte restait dans une large mesure occulté, personne (autant dire) n’en parlait jamais – mais le contact vivant avec les sources profondes du rêve, qui alimentent les grandes visions et les grands desseins, n’avait jamais encore (à ma connaissance) été perdu. Il semblerait que dès à présent nous soyons déjà entrés dans une époque de dessèchement, où cette source est non point tarie certes, mais où l’accès à elle est condamné, par le verdict sans appel du mépris général et par les représailles de la dérision. »[4]
Si l’on cherche le livre entier que Fermat aurait consacré à la science des nombres, on trouvera beaucoup de choses dans l’Arithmetica de 1670 qui icontient 48 observations très stimulantes. La pépite (sur le théorème) qui y figure est une galéjade qui laisse pantois. Jamais on n’avait vu, jamais plus on ne verra, un génie fût-il universel livrer la démonstration d’un puissant théorème sous forme d’une affirmation qui laisse tant à penser : « J'en ai réellement mis à nu l'explication tout à fait étonnante que la marge trop étroite ne contiendrait pas ».
« La marque infaillible du sublime, c’est quand nous sentons qu’un discours nous laisse beaucoup à penser, qu’il fait d’abord un effet sur nous, auquel il est bien difficile, sinon impossible, de résister, et qu’ensuite le souvenir nous en dure, et ne s’efface qu’avec peine. » Traité du Sublime (auteur inconnu, peut-être Longin).
« Le génie n’est pas imitable, il est incommunicable. On ne peut pas le transmettre parce que le génie lui-même serait incapable d’en donner les règles, c’est du côté du sublime plutôt que du beau. » Hélène Frappat.
Être mathématicien professionnel a des avantages et des inconvénients. Parmi ces derniers l’un émerge : vous ne pensez plus pratiquement qu’à votre travail, votre esprit, consciemment ou inconsciemment, y est occupé jour et nuit. Quant à l'étude du cas Fermat, de nombreux mathématiciens et historiens s’y sont penchés, mais un consensus ne s’est jamais fait. Allez-vous perdre votre temps à l’étudier ? Si vous êtes un simple amateur, confiant, objectif et audacieux, le problème se pose différemment, vous constatez d’abord qu’aucun des arguments avancés par les commentateurs sceptiques n'est sérieux. Leur assemblage l'est d'autant moins et tout l’édifice s'écroule dès que vous ôtez les plus mauvais :
a) Fermat s’était déjà trompé avec les nombres de la forme 22n + 1 (nous verrons plus loin de quelle façon et dans quel but ce fut un coup de bluff de sa part) ; b) Il a dû encore se tromper, il s’en est aperçu plus tard, mais puisque ces observations « étaient réservées à son seul usage » (...) il n’a pas jugé utile de rectifier ; c) Il ne disposait pas de nos outils modernes.
Si donc vous êtes juste un amateur très attentionné, vous voyez immédiatement qu’il y a anguille sous roche. Alors vous vous documentez. Longtemps si vous êtes un passionné. Une remarque très vite vous est venue à l’esprit : ces commentateurs semblent être partis de l’a priori que Fermat n’avait pu trouver une preuve, puis ont cherché tout ce qui pourrait les conforter dans cette idée, agrégeant leurs arguments en un seul bloc pour en faire une quasi-certitude – quand ce n'est une négation complète. Vous vous posez alors pas mal de questions sur l’honnêteté intellectuelle de certains savants. L’amateur que vous êtes se dit : « Tout ceci n’est qu’un écran de fumée », smoke and mirrors disent les Anglo Saxons. Fermat dont la véritable profession est magistrat, a toujours considéré l’émulation comme le meilleur moteur dans ses recherches arithmétiques. Il aura tout essayé, pendant 19 ans il a mis au défi 7 de ses correspondants : prouver, ou infirmer, sa fausse conjecture sur les nombres de Fermat. Mais aucun n'a vraiment donné suite.
L’attitude que l’on a, face au ‘’Dernier théorème’’ (on dirait le titre d’un roman, ce qu’il est en effet) dépend donc de l’a priori choisi au départ. Si l’on choisit celui qui est favorable, on se dit que Fermat, pédagogue et facétieux à la fois, et honnête homme s'il en est, n’a pas dû en rester là. On est prêt alors à chercher assidûment tous les indices qu’il aurait pu nous laisser, ne négligeant aucune piste. Eric Temple Bell croyait en une preuve de Fermat et pensait que la civilisation probablement s'éteindrait avant que le Dernier théorème soit résolu. Il n'était pourtant pas totalement exclu que le théorème soit un jour prouvé par une méthode très complexe : ce fut le cas, et on découvrira d'autres preuves complexes. Vouloir à tout prix croire que Pierre de Fermat n’a pu trouver une preuve empirique, donc beaucoup courte que celle de Wiles en 1994, est une mal-mesure criante de la science des nombres et plus généralement de la méthode scientifique.
Mathématique et poésie
Blaise Pascal, dans les Pensées, distingue l'esprit de géométrie et l'esprit de finesse.
À un pur mathématicien qui n’est que mathématicien, les plus grandes évidences toujours échapperont. J’ai lu très peu de mathématiciens en qui, en dehors de leurs mathématiques, on pouvait accorder toute confiance. Seul peut raisonner clairement le mathématicien qui a gardé son esprit d’enfance, ce doit être un poète, qui jamais ne bride son imagination créatrice. Etienne Klein dit à propos d'Einstein : « C'est peut-être ce que j'admire le plus chez lui. Cette capacité qu'il avait à se poser des questions toutes simples, des questions d'enfant, et à leur trouver des réponses élaborées avec toute la rigueur d'un cerveau d'adulte. » Souvenons-nous aussi que Fermat a écrit de la poésie (en plusieurs langues). De même Giordano Bruno. Pensons aussi à l’inoubliable logicien qu’était Lewis Caroll, auteur de ‘’Alice au pays des merveilles’’ et de “De l'autre côté du miroir’’. Pensons à Jacques Roubaud, écrivain et mathématicien, membre de l'Oulipo, joueur de go et poète bien connu des mathématiciens, qui concilie opportunément « l'esprit de géométrie et l'esprit de finesse ». Puis remarquons que Catherine Goldstein, chercheuse en mathématiques et historienne, qui a toujours dit contrairement à une ribambelle de sachants que l’existence d’une preuve du Théorème de Fermat par Fermat lui-même n’avait rien d’improbable, avait pour père un poète, Isidore Isou (1925-2007), qui fut aussi peintre, romancier, dramaturge, économiste… N'oublions pas non plus les écrits littéraires d'Alexandre Grothendieck (voir infra).
Selon le mathématicien Jacques Hadamard la rêverie, l’imagination, joue un grand rôle dans l’invention mathématique, c’est souvent en imaginant un chemin nouveau que les plus grands chercheurs ont «vu» une solution jusqu'alors inaccessible. Le mot “théorème” vient d’ailleurs du grec ancien θεώρημα (theốrêma en latin) : une proposition objet de contemplation, de méditation. Selon Bachelard l’imagination confère surtout le pouvoir de nous libérer des images premières fournies par la perception en les déformant, en les changeant : « Le vocable fondamental qui correspond à l’imagination, ce n’est pas image, c’est imaginaire. » (L’air et les songes. Paris, José Corti, p. 7).
La mathématique s’occupe des quantités et des formes, elle n’est pas le tout. La raison ne doit pas être gouvernée par la seule logique algébrique mais par la logique générale, abstraite. Les mathématiciens ont implicitement postulé qu’une vérité purement algébrique devait être une vérité générale. La confusion est si énorme, l'erreur si grossière, qu'on ne peut que s'émerveiller de l'unanimité avec laquelle elle fut acceptée. De même un axiome mathématique ne peut être un axiome d’une vérité générale. Les mathématiciens ont aussi cru bon d’appliquer le terme ‘’analyse’’ à un domaine de leur discipline, considérant ainsi que les mots tirent leur valeur de leur application. Essayez, si vous ne craignez de vous faire écharper, d’expliquer cela à un pur mathématicien qui ne raisonne qu’avec sa raison algébrique. L'assujettissement à un biais cognitif aussi pernicieux empêche tout imaginal de prendre sa place dans une réflexion englobante.
Extrait de la lettre de Fermat à Claude Clerselier à propos de la démonstration de Descartes sur la réfraction (21 mai 1662) : « […] Car si cette demonstration est dans les regles des demonstrations certaines et infaillibles, il n’est rien de plus vray, sinon que ceux qui n’en sont pas convaincus ne l’entendent point. La qualité essentielle d’une demonstration est de forcer à croire, de sorte que ceux qui ne sentent pas cette force, ne sentent pas la demonstration mesme, c’est à dire, qu’ils ne l’entendent pas. […] ».
Wiles et Fermat
Réflexion d’un journaliste à Andrew Wiles après sa découverte de 1995 : « Donc la preuve originale de Fermat est toujours présente quelque part. » Réponse : « Je ne crois pas que Fermat avait une preuve. Je pense qu’il s’est trompé en disant qu’il avait une preuve. Mais ce qui a rendu ce problème spécial pour les amateurs, c’est qu’il existe une infime possibilité qu’il existe une preuve élégante du XVIIe siècle ». Si j’avais été à sa place j’aurais certainement répondu la même chose (peut-être même exactement), c’eût été très confortable pour moi, ces sept années d’efforts soutenus n’auraient pas été vaines (même si ces travaux ont beaucoup enrichi les math, mais c’est une autre question). Wiles est un grand mathématicien, tout comme Fermat. Il est plaisant de noter que le magistrat Pierre de Fermat, qui ne pouvait gaspiller le peu de son temps disponible à détailler tous ses calculs (ne gardant quasiment jamais une copie d’un travail transmis à un correspondant), obstiné qu’il était d’aller toujours plus loin, se disait « l’homme le plus paresseux du monde ». Tous deux, chacun à leur façon, avec les outils de leur temps, ont fait faire aux mathématiques des avancées considérables. Ces deux génies sont un peu comme deux jumeaux. Andrew a pourtant un handicap, c’est un mathématicien complètement dans son temps, il a dû dans sa formation assimiler énormément de mathématiques du vingtième siècle, en inventer beaucoup de nouvelles, peut-être que s’il avait vécu à l’époque de Fermat, obligé qu’il eût été de se satisfaire d’une mathématique plus pure, qui tente d’appréhender au plus près les relations profondes entre les nombres, et donc difficile à saisir, il aurait pu s'approcher du maître. Les Anciens n’avaient pas encore l’esprit encombré de cette multitude de données complexes que les Modernes ont été obligés d’assimiler pour perpétuer le progrès technologique. Wiles a été tellement émerveillé par son succès après tous ses efforts que toute pensée relative à l’existence d’une preuve du XVIIe siècle ne pouvait qu’achopper aux contours de son esprit, comblé par sa découverte ; rien ne devait altérer sa joie. On peut tenter d'imaginer ce qu'elle a pu être, quand il cherche les mots pour l'exprimer l'émotion est si forte que les larmes lui montent aux yeux. La course au ‘’Dernier Théorème‘’ fut une longue quête de 324 ans. Son histoire fut tellement excitante pour les mathématiciens qui pourtant n'ont jamais pu percer le secret de Fermat que la légende urbaine qui y a cohabité depuis le début pour conjurer un dépit irritant, logiquement devrait poursuivre tranquillement sa route. Quel sujet passionnant, mêlant sociologie, philosophie, psychologie, historiographie, quelle admirable leçon de pédagogie aussi : après l'avoir entrouverte, Pierre fermat la porte à tous les sachants.
Suite (2/4) : Premier maillon : le coup de bluff




